Research

Here are some of my most important research projects and their key findings:

Information, Logic, and Inference in the Analysis of Complex Networks

PhD Thesis, Georg-August Universität Göttingen, 2023

My doctoral thesis develops mathematical methods for analyzing information processing in complex networks, integrating insights from information theory and formal logic. It also introduces statistical inference techniques for testing and estimating information flow.

Bits and Pieces: Understanding Information Decomposition from Part-Whole Relationships and Formal Logic

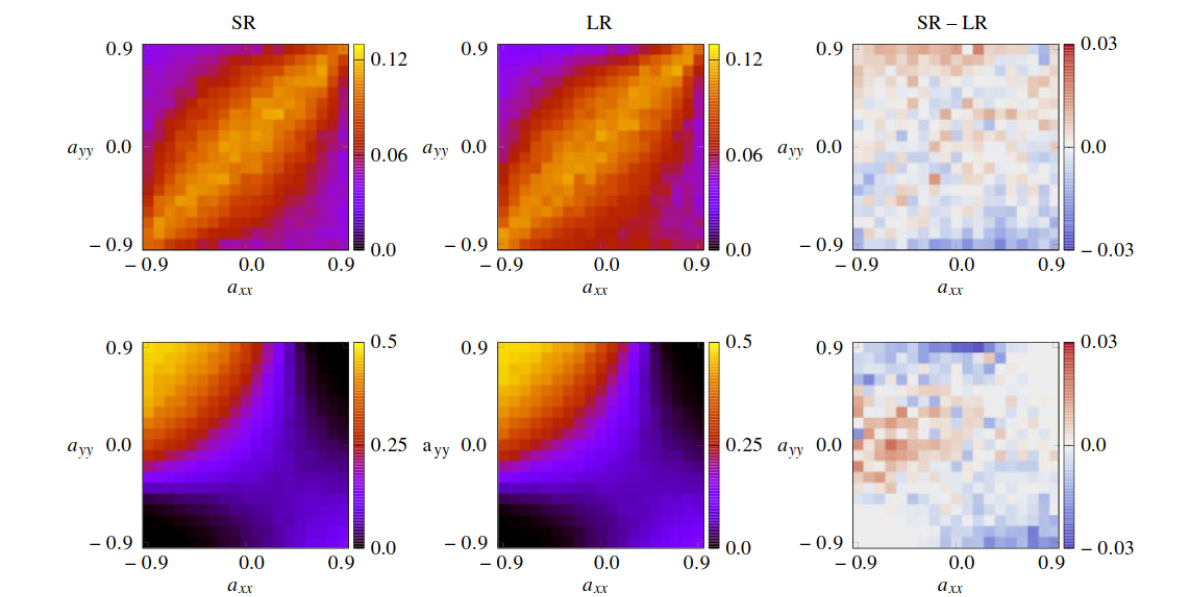
A. J. Gutknecht, M. Wibral, A. Makkeh, Proceedings of the Royal Society A, 2021

PID conceptual framework

This paper establishes a mathematical foundation for Partial Information Decomposition (PID) using mereology (the study of part-whole relationships) and formal logic. PID extends Shannon information theory by quantifying how information about a target variable is distributed across multiple sources. Specifically, it distinguishes information that is unique to certain sources, redundantly shared among them, or synergistically generated through their interactions. PID is highly relevant to all areas of complexity science, as it provides a mathematical basis for defining and quantifying key concepts such as emergence or the complexity of representations in neural networks.

From Babel to Boole: The Logical Organization of Information Decompositions

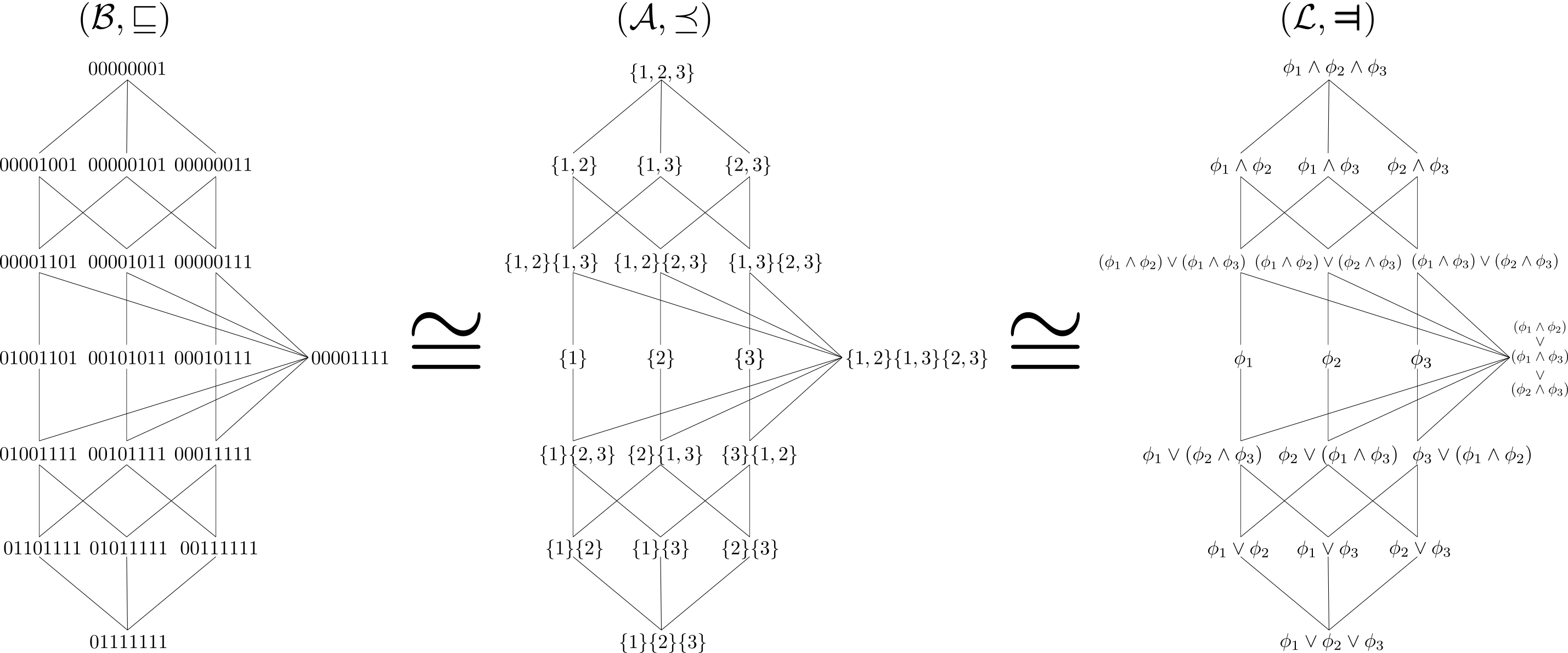
A. J. Gutknecht, A. Makkeh, M. Wibral, arXiv preprint arXiv:2306.00734, 2023

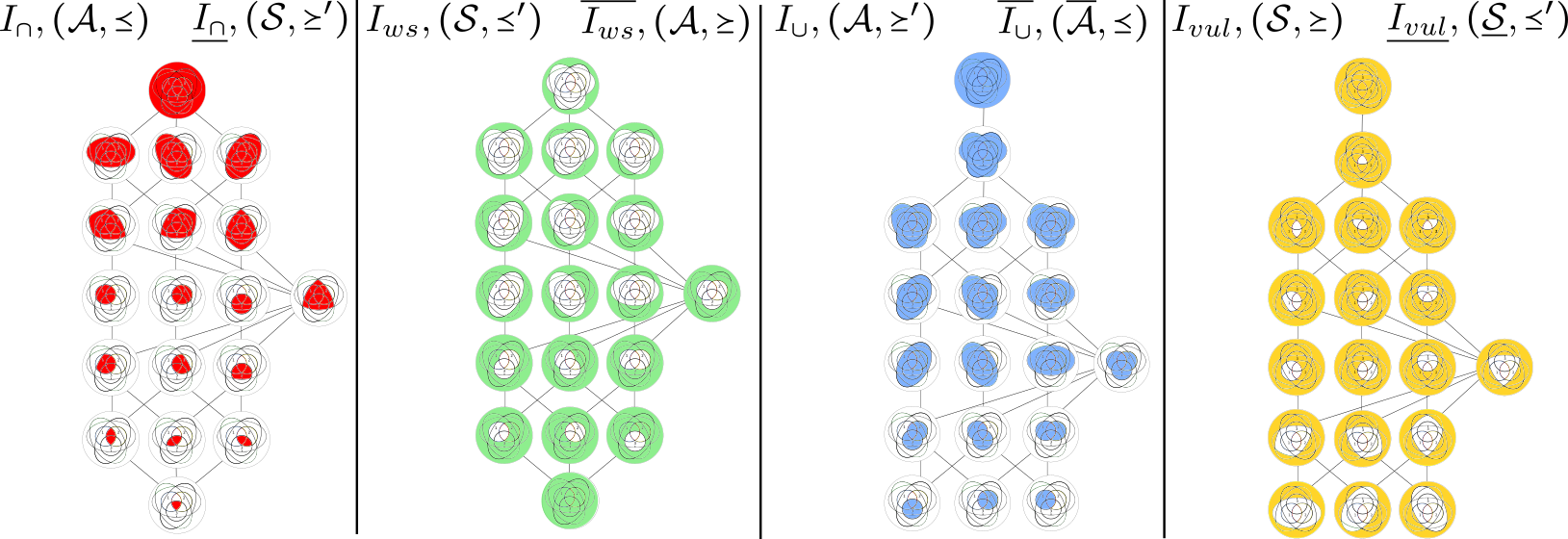
Logical scheme diagram

This work expands on the ideas in Bits and Pieces by introducing a unifying framework for Partial Information Decomposition based on Boolean functions. It identifies PID-inducing concepts—such as redundancy, synergy, and union information—as logical conditions on these functions. The framework clarifies the relationships between different PID approaches and introduces novel PID inducing concepts such as “vulnerable information”, thus offering new insights into the structure of information decomposition.

Sampling Distribution for Single-Regression Granger Causality Estimators

A. J. Gutknecht, L. Barnett, Biometrika, 2023

Granger causality diagram

This paper contributes to the statistical theory of linear information flow. It analytically derives the sampling distribution of a particularly efficient class of Granger causality estimators known as “single regression” estimators. It also construct valid statistical tests based on the derived distributions.